对快速排序的理解?如何实现?应用场景?
对快速排序的理解?如何实现?应用场景?
一、是什么
快速排序(Quick Sort)算法是在冒泡排序的基础上进行改进的一种算法,从名字上看就知道该排序算法的特点是快、效率高,是处理大数据最快的排序算法之一
实现的基本思想是:通过一次排序将整个无序表分成相互独立的两部分,其中一部分中的数据都比另一部分中包含的数据的值小
然后继续沿用此方法分别对两部分进行同样的操作,直到每一个小部分不可再分,所得到的整个序列就变成有序序列
例如,对无序表49,38,65,97,76,13,27,49进行快速排序,大致过程为:
首先从表中选取一个记录的关键字作为分割点(称为“枢轴”或者支点,一般选择第一个关键字),例如选取 49
将表格中大于 49 个放置于 49 的右侧,小于 49 的放置于 49 的左侧,假设完成后的无序表为:{27,38,13,49,65,97,76,49}
以 49 为支点,将整个无序表分割成了两个部分,分别为{27,38,13}和{65,97,76,49},继续采用此种方法分别对两个子表进行排序
前部分子表以 27 为支点,排序后的子表为{13,27,38},此部分已经有序;后部分子表以 65 为支点,排序后的子表为{49,65,97,76}
此时前半部分子表中的数据已完成排序;后部分子表继续以 65 为支点,将其分割为{49}和{97,76},前者不需排序,后者排序后的结果为{76, 97}
通过以上几步的排序,最后由子表{13,27,38}、{49}、{49}、{65}、{76,97}构成有序表:{13,27,38,49,49,65,76,97}
二、如何实现
可以分成以下步骤:
- 分区:从数组中选择任意一个基准,所有比基准小的元素放在基准的左边,比基准大的元素放到基准的右边
- 递归:递归地对基准前后的子数组进行分区

用代码表示则如下:
1 | function quickSort (arr) { |
快速排序是冒泡排序的升级版,最坏情况下每一次基准元素都是数组中最小或者最大的元素,则快速排序就是冒泡排序
这种情况时间复杂度就是冒泡排序的时间复杂度:T[n] = n * (n-1) = n^2 + n,也就是O(n^2)
最好情况下是O(nlogn),其中递归算法的时间复杂度公式:T[n] = aT[n/b] + f(n),推导如下所示:
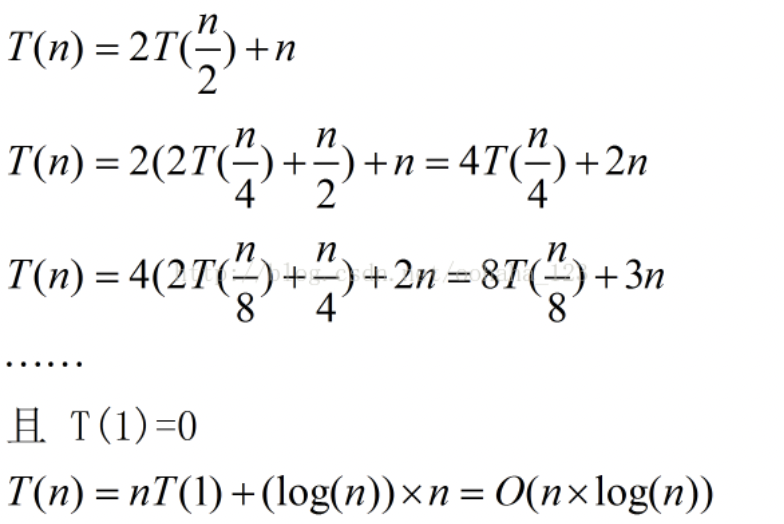
关于上述代码实现的快速排序,可以看到是稳定的
三、应用场景
快速排序时间复杂度为O(nlogn),是目前基于比较的内部排序中被认为最好的方法,当数据过大且数据杂乱无章时,则适合采用快速排序